Download PDF Contact Author
The Maxwell equation and the derived d ‘Alembert wave equation cannot provide the answers to the above questions. We require a velocity vector in the Maxwell formulations. The talk presents the proof that the simultaneous vector crossproduct equations.
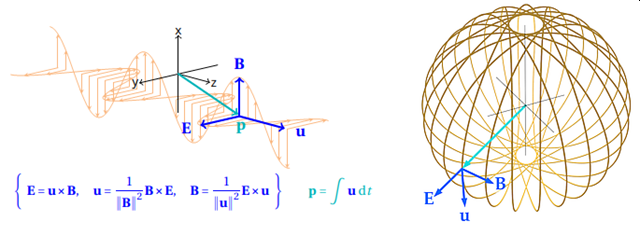
{ E = u × B; u = (B×E)/∥B∥^2; B= ( E×u)/∥u∥^2} — (1)
are a powerful reformulation of the Maxwell equations in vacuum, if u , B and E are functions of time only, therefore (1) also describes EM-waves in 1D (radio waves and photons), 2D and 3-dimensions (particles). The figure sketches a three dimensional wave, here we note that E is always radiant and B and u tangential.
On the premise that equation set (1) also describes wave action (here electric action) it must follow that a purely mathematical derivation for ϵ _0 and μ_0,in terms of e and h, should emerges from (1), indeed it is so and is demonstrated. Leveraging (1) to describe flux-waves requires the equivalent expression s for ϵ_f and μ_f, and after deriving these the Planck energy equivalence E=hf emerges from (1). The solutions to (1) set in flux are easily quantifiable; for the 3D-wave the following are identifiable: up/down, spin on two axes, charge polarity, and path closure 2 nπ, with n an integer. The proposed description for particles is congruent to the Bohm ˗de Broglie interpretation of quantum mechanics and a nonlocal hidden variable; this is discussed too.

Comments and Replies