In unstressed vacuum EM traveling plane waves propagate on a linear path. Question: Can an electromagnetic wave travel on a closed and curved 3-dimensional path, say a spherical-like path, and how to formulate such a paths without using superpositioning? Furthermore, the Maxwell equations are field (flux per area) equations which begs the second question: Are there equivalent potential (flux per distance) and flux equations to model EM-potential and EM-flux waves? This presentation answers both questions in the affirmative from a purely mathematical point of view. The new insight developed here could provide a tool box to envision Maxwellian solitons, a possible aid, and supportive view, to further the understanding of particles. 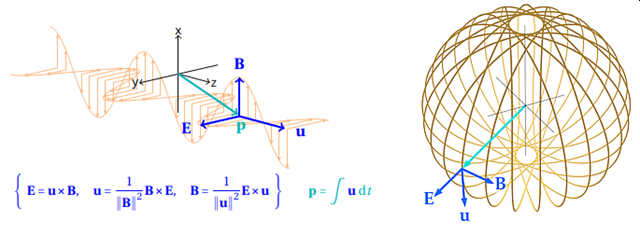The Maxwell equation and the derived d 'Alembert wave equation cannot provide the answers to the above questions. We require a velocity vector in the Maxwell formulations. The talk presents the proof that the simultaneous vector crossproduct equations. { E = u × B; u = (B×E)/∥B∥^2; B= ( E×u)/∥u∥^2} --- (1) are a powerful reformulation of the Maxwell equations in vacuum, if u , B and E are functions of time only, therefore (1) also describes EM-waves in 1D (radio waves and photons), 2D and 3-dimensions (particles).   The figure sketches a three dimensional wave, here we note that E is always radiant and B and u tangential. On the premise that equation set (1) also describes wave action (here electric action) it must follow that a purely mathematical derivation for ϵ _0 and μ_0,in terms of e and h, should emerges from (1), indeed it is so and is demonstrated. Leveraging (1) to describe flux-waves requires the equivalent expression s for ϵ_f and μ_f,  and after deriving these the Planck energy equivalence E=hf emerges from (1). The solutions to (1) set in flux are easily quantifiable; for the 3D-wave the following are identifiable: up/down, spin on two axes,  charge polarity, and path closure 2 nπ, with n an integer.  The proposed description  for particles is congruent to the Bohm ˗de Broglie interpretation of quantum mechanics and a nonlocal hidden variable; this is discussed too.

@Online{Vrba-2023-1823,
   author    = {Vrba, Anton Lorenz},
   title     = {Particles as Maxwellian Solitons},
   year      = {2023},
   url       = {https://neophysics.org/p/1823},
   urldate   = {2024-09-16},
}

Abstract We construct a simple EPR experiment: A source of circular polarised entangled photon pairs are sent to Alice and Bob. Alice intersects her beam with an asymmetrical 75:25 polariser, constructed from a cascade of three polarisers, but does no observation. Question: Are the photons Bob receives skewed 25:75? Using a nonlocal classical construct  demonstrates from Maxwellian principles  a universal conservation phenomenon, as predicted by Noether’s Theorem.   The analysis confirms the Bell inequality and the outcome that Bob’s observations are skewed 25:75 which contrasts the expected 50:50 distribution that quantum mechanics predict.

@Online{Vrba-2023-1782,
   author    = {Vrba, Anton Lorenz},
   title     = {Can Alice influence Bob? Yes she can, Maxwell demands it and Noether predicted it; A nonlocal Maxwellian explanation of the EPR experiment.},
   year      = {2023},
   url       = {https://neophysics.org/p/1782},
   urldate   = {2024-09-16},
}

Abstract: In 1926, Erwin Schrödinger proposed an equation that describes the wave function for the electron orbits of  the Hydrogen atom. The Schrödinger equation is accepted as a postulate because of unclear and possible erroneous steps in his methods. Addressing the erroneous steps, we show that the Schrödinger equation extracts only the stable trajectories from all possible trajectories that are solutions of the Hamilton-Jacobi equation. This approach applied to a Hydrogen atom leads to the following results: (1) Bohr orbits are stable, (2) the electron’s spin in an atom is precessing; (3) the energy of the precessional motion on Bohr orbits satisfies the Rydberg’s formula.

@Online{Sotina-2023-1738,
   author    = {Sotina, Nina},
   title     = {The Schrödinger equation from the point of view of the theory of stability},
   year      = {2023},
   url       = {https://neophysics.org/p/1738},
   urldate   = {2024-09-16},
}

Abstract Waves of all types are described mathematically using partial differential equations. Here, departing from this tradition, I describe waves using a novel system of three simultaneous vector algebraic equations: $\mathscr{M}(\vb u,\vb a,\vb r) = \big\{\vb r= \vb u \cross \vb a;\,$ $\vb u= (\vb a \cross \vb r)/\norm{\vb a}^2;\,$ $\vb a = (\vb r \cross \vb u)/\norm{\vb u}^2 \big\}$ which define Maxwellian wave dynamics for any fields $\vb a$ and $\vb b$ that support wave action and $\vb u$ a velocity vector. That is $\mathscr{M}(\vb u,\vb B,\vb E)$ is a novel reformulation of the Maxwell equations in vacuum. Furthermore, the expressions for the permittivity $\epsilon_0$, permeability $\mu_0$ and the magnetic flux density $\vb B$, in terms of action $h$, elementary charge $e$ and speed of light $c$, are obtained by manipulating $\mathscr{M}$ with the assumption that an EM-wave has action and transports charge. As an application of $\mathscr{M}(\vb u,\vb B,\vb E)$ I show that three dimensional spherical EM-wave structures do exist, in theory at least. They are stationary with finite dimensionality and could provide the basis for describing EM-solitons, which in turn could be used to describe many natural phenomena, including ball lightning among others. Instead of working with fields I reformulate $\mathscr{M}$ in terms of flux vectors $\vb A$ and $\vb R$. Using $\mathscr{M}(\vb u, \vb A, \vb R)$ I describe rotary waves (propeller-like instead of ripples on a pond) and show that rotary waves could be the basis to describe particles, physically, as solitons in terms of Maxwellian wave dynamics.

@Online{Vrba-2022-1721,
   author    = {Vrba, Anton},
   title     = {General Maxwellian Dynamics:  Maxwellian Solitons as particles},
   year      = {2022},
   url       = {https://neophysics.org/p/1721},
   urldate   = {2024-09-16},
}

Abstract: History records how Maxwell unified the work of Gauss, Faraday and other pioneers which led to the prediction of electromagnetic waves, because the d’Alembert wave equation is derivable from the Maxwell equations. In contrast, I begin with three simultaneous algebraic-vector equations and show that these define the Maxwell equations and the properties of vacuum. Now instead of using the d’Alembert wave equation to define electromagnetic waves, we can use the three simultaneous algebraic-vector equations to define wave structures that can be three dimensional, e.g. ball lightning. Also, it shows that the electromagnetic phenomenon and the properties of the vacuum are dictated by mathematical requirements.

@Online{Vrba-2022-1576,
   author    = {Vrba, Anton Lorenz},
   title     = {The mathematical origin of the Maxwell equations},
   year      = {2022},
   url       = {https://neophysics.org/p/1576},
   urldate   = {2024-09-16},
}

When:	2022-11-12 19:00 (GMT)
Where:	Online - Zoom link: t.b.a
Who:	Anton Vrba

httpv://youtu.be/2OsIUtz3opA Agenda:

1. Aims and Objects
2. Introducing the Website
3. Introding the online journal: Harbingers of Neophysics

If you wish to participate in this venture your feedback is important now.

@Online{Vrba-2022-1228,
   author    = {Vrba, Anton Lorenz},
   title     = {Grand Opening; Introduction to Harbingers of Neophysics},
   year      = {2022},
   url       = {https://neophysics.org/p/1228},
   urldate   = {2024-09-16},
}